Instructional Unit- Circles

The following investigations can be enhanced by using a program such as GSP. Keep in mind that GSP can help explore and make hypothesis, but should never be solely used to prove something.

Angles in a circle:

Students can construct 4 different circles, and explore the relationship between the angle measure and the arc length the angle subtends. The vertex of an angle can be the center of the circle, a point inside the circle but not the center, on the circle, or outside the circle as shown below.

First one might begin with simple explorations, such as what happens as the angle measure is changed in each of the 4 circles?

(GSP can measure the angle you are looking at, as well as the arc the angle intercepts.)

Then, the investigations may get deeper.

How is the angle measure related to the arc for the vertex that is the center of the circle?

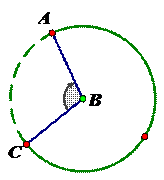
How many arcs are created when the vertex of an angle is inside the circle, but is not the center of the circle? What is the relationship between the angle measure and the arc it intercepts?

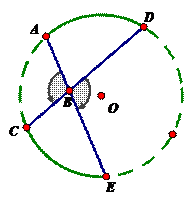
How is the angle measure related to the arc for the vertex that on the circle?

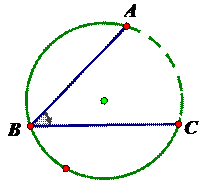
How many arcs are created when the vertex of the angle is outside of the circle? What is the relationship between the angle measure and the arcs it intercepts?

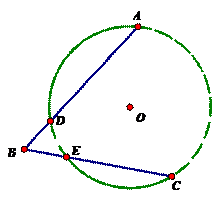
Changes in circumference and area as the radius is changed:

Before you construct some circles, first think about the following questions:

1) What do you think happens to the circumference of a circle if the radius is doubled? Halved?

2) What do you think happens to the area of a circle if the radius is doubled? Halved?

Now, you may begin exploring these concepts using GSP. Keep in mind the measurements you get are strictly experimental, and cannot be used to prove anything.

Start with an arbitrary circle of radius AB, and find the radius length, circumference, and area.

Then, double the radius of the original circle, and find the same measurements.

Lastly, create a circle with half the radius of the original circle, and take some measurements.

Were your answers to questions 1) and 2) correct?

Now, using what you have discovered, what do you think happens to the volume of a sphere when the radius is doubled or halved? (V= (4/3) )

We can explore this using GSP, and come to some conclusions using algebra. Was your prediction right? What does happen to the volume of a sphere when the radius is doubled or halved?

Common Ratio of Circles

Have your students use GSP to explore the ratio of the circumference to the diameter.

What is the ratio? Do you think it is the same for all circles? How do you think the formulas involving circles and spheres came about?

Here we might throw in some history about pi. In mathematics, history can be used for several different purposes. History can be used as a “hook” when discussing a mathematical topic, such as pi. Using history in the classroom may also provide connections from mathematics to the real world.

Mathematicians have used the ratio of pi since the very basic mathematics came about. There is no for sure answer as to what group of people discovered the ratio first. The Babylonians, who were around before the Egyptians, said the circumference of a circle was 3 times the diameter (in this case, π=3). It is rumored that the Egyptians may have used pi when constructing their pyramids beginning in the 2000’s B.C. In general, the Egyptians used the “square of 8/9 of the diameter” to represent the ratio. This gives an approximate value of 3.1605 for pi.

Archimedes of Syracuse is the first recorded mathematician to theoretically calculate pi around 240 B.C. He said that 223/71 < π < 22/7. Archimedes actually used regular polygons that were inscribed in circle to estimate the area of circles.

In China around 480 B.C., mathematician Tsu Ch’ung-chih gave an approximation of 355/113, which is 3.1415929, and correct to six decimal places!

As time progressed, many mathematicians and scholars made their attempts at calculating the value of pi. With technology, the calculation of pi has become more and more precise. In 1986, members of the NASA Ames Research Center ran a supercomputer for 28 hours to calculate pi to 29, 360,000 digits! Sadly, the exact value of pi will never be known, as it is an irrational number.

Once the students get some history of pi, you can incorporate fun activities. These activities can range from baking a pi and taking measurements, and then of course eating it! For younger ages, the decimal representation of pi can be created with a chain link. Each digit, 1-9, can be represented by a different color paper, and a chain can be made out of links. Older students can derive the value of pi themselves by doing the above activity, “Common Ratios of Circles.”

Sources:

Exploartions: InterMath

History of pi: Eves, H. (1990). An introduction to the history of mathematics, 6^th Edition. Pacific Grove: Thompson Learning, Inc.